動いているおもりが持つエネルギーは「放した高さ」×「おもりの重さ」で考える
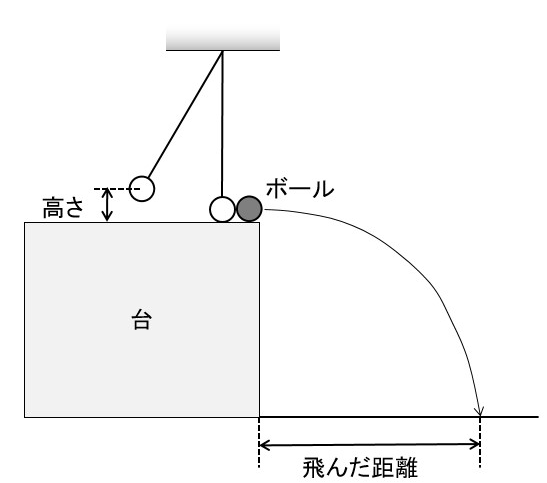
【解説】
1. 表のA〜Fから、くらべたいことがらだけが違う実験を1組ずつ選び、ボールが飛んだ距離がどのように変化したか確かめます。
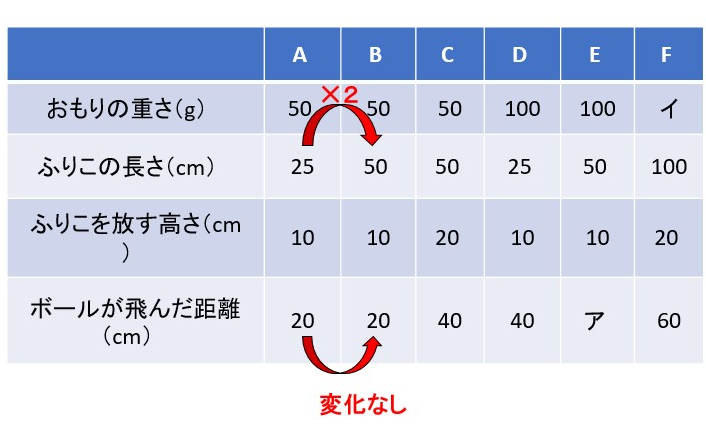
たとえばPの場合、くらべたいのは「ふりこの長さ」です。つまりふりこの長さ「だけ」が違う2つの実験をA〜Fから選び、その2つの実験をくらべればいいのです。
P. 実験AとBをくらべます。おもりの重さ、ふりこを放す高さは同じで、ふりこの長さだけがBはAの2倍になっていますが、ボールが飛んだ距離は変わっていません。
よってこたえは ✗ です。
Q. 実験AとDをくらべます。ふりこの長さ、ふりこを放す高さは同じで、おもりの重さだけがDはAの2倍になっていますが、ボールが飛んだ距離も同じように2倍になっています。
よってこたえは ○ です。
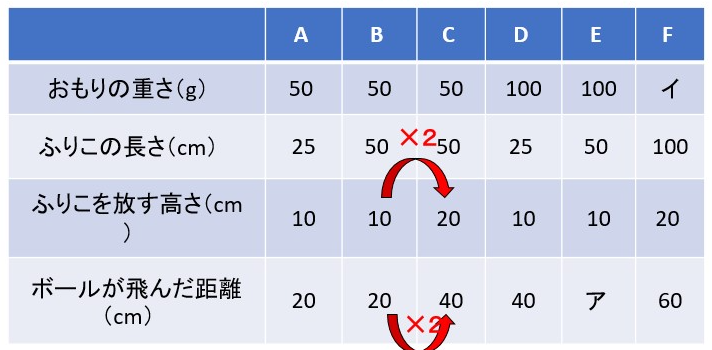
R. 実験BとCをくらべます。おもりの重さ、ふりこの長さは同じで、ふりこを放す高さだけがCはBの2倍になっていますが、ボールが飛んだ距離も同じように2倍になっています。
よってこちらもこたえは ○ ですね。
2. 1.から、おもりが飛んだ距離は「おもりの重さ」「ふりこを放す高さ」に比例することがわかりました。つまり「おもりの重さ✕ふりこを放す高さ」に比例するということですね。
A.の実験は「おもりの重さ✕ふりこを放す高さ」が「 50 ✕ 10 = 500 」となっていて、このときボールが飛んだ距離は20cmとなっています。
E.の実験では「おもりの重さ✕ふりこを放す高さ」が「 100 ✕ 10 = 1000 」となっていて、A.の実験の2倍です。
つまりアは 20 ✕ 2 = 40 ですね。 こたえ 40
F.の実験では
「おもりの重さ✕ふりこを放す高さ」が「 イ ✕ 20 」となっていて、ボールが飛んだ距離はA.の実験の3倍です。
つまり 「 イ ✕ 20 = 500 ✕ 3 = 1500 となります。
だからイは 1500 ÷ 20 = 75 となります。 こたえ 75
このように
ボールが飛んだ距離は「おもりの重さ」「ふりこを放す高さ」に比例するから
「おもりの重さ✕ふりこを放す高さ」に比例する!
と考えるとぐっと簡単に解けるようになります。